Bab 4 : PROGRAM LINIER

Nama : Safta Sabrina // X-MM No. 27

PROGRAM LINIER

• A.PENGERTIAN PROGRAM LINER

Program linear adalah suatu metode penentuan nilai optimum dari suatu persoalan linear. Nilai optimum (maksimal atau minimum) diperoleh dari nilai dalam suatu himpunan penyelesaiaan persoalan linear. Di dalam persoalan linear terdapat fungsi linear yang bisa disebut sebagai fungsi objektif. Persyaratan, batasan, dan kendala dalam persoalan linear merupakan sistem pertidaksamaan linear.

SISTEM PERTIDAKSAMAAN LINEAR DUA VARIABEL

Pertidaksamaan linear adalah pertidaksamaan yang peubah bebasnya berbentuk linear (pangkat satu). Kalian tentu masih ingat bentuk-bentuk di bawah ini.

1. 2x ≥ 4; pertidaksamaan linear satu peubah
   2. 3x + y < 0; pertidaksamaan linear dua peubah
   3. x – 2y ≤ 3; pertidaksamaan linear dua peubah
   4. x + y – 2z > 0; pertidaksamaan linear tiga peubah

Dalam postingan perpustakaan online kali ini kita hanya akan mempelajari pertidaksamaan linear dengan dua peubah. Gabungan dari dua atau lebih pertidaksamaan linear dua peubah disebut sistem pertidaksamaan linear dua peubah.

Contoh sistem pertidaksamaan linear dua peubah adalah sebagai berikut.
3x + 8y ≥ 24,
x + y ≥ 4,
x ≥ 0,
y ≥ 0.

1. Daerah Himpunan Penyelesaian Pertidaksamaan Linear Dua Peubah

Penyelesaian suatu pertidaksamaan linear dua peubah adalah pasangan berurut (x,y) yang memenuhi pertidaksamaan linear tersebut. Himpunan penyelesaian tersebut dinyatakan dengan suatu daerah pada bidang kartesius (bidang XOY) yang diarsir. Untuk lebih memahami daerah himpunan penyelesaian pertidaksamaan linear dua peubah, pelajari contoh-contoh berikut.

Contoh :
Tentukan himpunan penyelesaian dari pertidaksamaan linear di bawah ini.
a. 2x + 3y ≥ 12             c. 4x – 3y < 12
b. 2x – 5y > 20                d. 5x + 3y ≤ 15

Penyelesaian:

1. Mula-mula dilukis garis 2x + 3y = 12 dengan menghubungkan titik potong garis dengan sumbu X dan sumbu Y.Titik potong garis dengan sumbu X berarti y = 0, diperoleh x = 6 (titik (6,0)).

Titik potong garis dengan sumbu Y berarti x = 0, diperoleh y = 4 (titik (0,4)).
Garis 2x + 3y = 12 tersebut membagi bidang kartesius menjadi dua bagian. Untuk menentukan daerah yang merupakan himpunan penyelesaian dilakukan dengan mengambil salah satu titik uji dari salah satu sisi daerah. Misalkan diambil titik (0,0), kemudian disubstitusikan ke pertidaksamaan sehingga diperoleh:

2 x0 + 3x 0 < 12
0 < 12

Jadi 0 ≥ 12 salah, artinya tidak dipenuhi sebagai daerah penyelesaian.

Jadi, daerah penyelesaiannya adalah daerah yang tidak memuat titik (0,0), yaitu daerah yang diarsir pada gambar di bawah ini.

1. Mula-mula dilukis garis 2x – 5y = 20 dengan menghubungkan titik potong garis di sumbu X dan sumbu Y.

Titik potong garis dengan sumbu X,  y = 0, diperoleh x = 10 (titik (10,0))
Titik potong garis dengan sumbu Y, x = 0, diperoleh y = –4 (titik (0,–4))

Garis 2x – 5y = 20 tersebut membagi bidang kartesius menjadi dua bagian. Untuk menentukan daerah yang merupakan himpunan penyelesaian dilakukan dengan mengambil titik uji dari salah satu sisi daerah. Misalkan diambil titik (0,0), kemudian disubstitusikan ke pertidaksamaan sehingga diperoleh:

2 x0 – 5 x0 > 20
0 > 20 (salah), artinya tidak dipenuhi.

Jadi, daerah penyelesaiannya adalah daerah yang tidak memuat titik (0,0), yaitu daerah yang diarsir pada gambar.

1. Mula-mula dilukis garis 4x – 3y = 12 dengan menghubungkan titik potong garis di sumbu X dan sumbu Y.

Titik potong garis dengan sumbu X maka y = 0 diperoleh x = 3 (titik (3,0))
Titik potong garis dengan sumbu Y maka x = 0 diperoleh y = –4 (titik (0,–4))

Garis 4x – 3y = 12 tersebut membagi bidang kartesius menjadi dua bagian. Untuk menentukan daerah yang merupakan himpunan penyelesaian dilakukan dengan mengambil salah satu titik uji dari salah satu sisi daerah. Misalkan diambil titik (0,0), kemudian disubstitusikan ke pertidaksamaan sehingga diperoleh:

4 x0 – 3x 0 < 12
0 < 12 (benar), artinya dipenuhi sebagai daerah penyelesaian.

Jadi, daerah penyelesaiannya adalah daerah yang memuat titik (0,0), yaitu daerah yang diarsir pada gambar di bawah.

1. Mula-mula dilukis garis 5x + 3y = 15 dengan menghubungkan titik potong garis di sumbu X dan sumbu Y.

Titik potong garis dengan sumbu X maka y = 0, diperoleh x = 3 (titik (3,0))
Titik potong garis dengan sumbu Y maka x = 0, diperoleh y = 5 (titik (0,5))

Garis 5x + 3y = 15 tersebut membagi bidang kartesius menjadi dua bagian. Untuk menentukan daerah yang merupakan himpunan penyelesaian dilakukan dengan mengambil salah satu titik uji dari salah satu sisi daerah. Misalkan diambil titik (0,0), kemudian disubstitusikan ke pertidaksamaan sehingga diperoleh:

5 x0 + 3x 0 ≤15
0 ≤ 15 (benar), artinya dipenuhi.

Jadi, daerah penyelesaiannya adalah daerah yang memuat titik (0,0), yaitu daerah yang diarsir pada gambar.

Berdasarkan contoh di atas, cara menentukan himpunan penyelesaian pertidaksamaan linear dengan dua peubah dapat dilakukan dengan langkah-langkah sebagai berikut:

1. Lukislah garis ax + by = c pada bidang kartesius dengan menghubungkan titik potong garis pada sumbu X di titik (c/a ,0) dan pada sumbu Y di titik (0,c/b ).
2. Selidiki sebuah titik uji yang terletak di luar garis dengan cara menyubstitusikannya pada pertidaksamaan. Jika pertidaksamaan dipenuhi (benar), maka daerah yang memuat titik tersebut merupakan daerah himpunan penyelesaian. Jika pertidaksamaan tidak dipenuhi (salah), maka daerah yang tidak memuat titik uji merupakan daerah himpunan penyelesaian.
3. Daerah Penyelesaian Sistem Pertidaksamaan Linear
4. Menentukan Daerah Penyelesaian Sistem Pertidaksamaan Linear
   Himpunan penyelesaian dari sistem pertidaksamaan linear dua peubah adalah himpunan titik-titik (pasangan berurut (x,y)) dalam bidang kartesius yang memenuhi semua pertidaksamaan linear dalam sistem tersebut. Sehingga daerah himpunan penyelesaianny amerupakan irisan himpunan-himpunan penyelesaian dari pertidaksamaan dalam sistem pertidaksamaan linear dua peubah itu. Agar kalian lebih mudah dalam memahami daerah penyelesaian dari sistem pertidak-samaan linear dua peubah, perhatikan contoh-contoh di bawah ini.

Contoh : Tentukan daerah himpunan penyelesaian dari sistem pertidaksamaan berikut.
a. 3x + 5y ≤ 15               b. x + y ≤ 6
x ≥ 0                    2x + 3y ≤ 12
y ≥ 0                              x ≥ 1
y ≥  2

Penyelesaian:

1. Mula-mula gambar garis 3x + 5y =15, x = 0, dan y =0
   Untuk 3x + 5y ≤ 15
   Pilih titik (0,0), kemudian substitusikan ke pertidaksamaan sehingga diperoleh:
   3x 0 + 5x 0 ≤ 15
   0 ≤ 15 (benar), artinya dipenuhi

Jadi, daerah penyelesaiannya adalah daerah yang memuatntitik (0,0)
Untuk x ≥ 0, pilih titik (1,1) kemudian disubstitusikan ke pertidaksamaan sehingga diperoleh:
1 ≥ 0 (benar), artinya dipenuhi.

Jadi, daerah penyelesaiannya adalah daerah yang memuat titik (1,1)
Untuk y ≥ 0, pilih titik (1,1) kemudian substitusikan ke pertidaksamaan sehingga diperoleh:
1 ≥ 0 (benar), artinya dipenuhi.
Jadi, himpunan penyelesaiannya adalah daerah yang memuat titik (1,1).

Daerah himpunan penyelesaian sistem pertidaksamaan merupakan irisan dari ketiga daerah himpunan penyelesaian pertidaksamaan di atas, yaitu seperti terlihat pada gambar berikut ini (daerah yang diarsir).

2. Mula-mula gambar garis x + y =6, 2x + 3y = 12, x = 1, dan y = 2. Untuk x + y ≤ 6, pilih titik (0,0), kemudian substitusikan ke pertidaksamaan sehingga diperoleh:

1 x0 + 1 x0 ≤ 6
0 ≤ 6 (benar), artinya dipenuhi.

Jadi, daerah penyelesaiannya adalah daerah yang memuat titik (0,0).
Untuk 2x + 3y ≤ 12, pilih titik (0,0), kemudian substitusikan ke pertidak-samaan sehingga diperoleh:

2 x0 + 3x 0 ≤ 12
0 ≤ 12 (benar), artinya dipenuhi.

Jadi, daerah penyelesaiannya adalah daerah yang memuat titik (0,0).Untuk x ≥ 1, pilih titik (2,1) kemudian disubstitusikan ke pertidaksamaan sehingga diperoleh 2 ≥ 1 (benar), artinya dipenuhi. Jadi, daerah penyelesaiannya adalah daerah yang memuat titik (2,1).

Untuk y ≥ 2, pilih titik (1,3) kemudian substitusikan ke pertidaksamaan sehingga diperoleh 3 ≥ 2 (benar), artinya dipenuhi. Jadi, himpunan penyelesaiannya adalah daerah yang memuat titik (1,3).

Daerah himpunan penyelesaian sistem pertidaksamaan tersebut merupakan irisan dari ketiga daerah himpunan penyelesaian pertidaksamaan di atas, yang seperti terlihat pada gambar di samping (daerah yang diarsir)

1. Menentukan Sistem Pertidaksamaan jika Daerah Himpunan Penyelesaian Sistem Pertidaksamaan Linear Dua Peubah Diketahui

Cara menentukan daerah himpunan penyelesaian dari sistem pertidaksamaan linear dua peubah telah dipelajari sebelumnya. Sekarang bagaimana menentukan sistem pertidaksamaan jika daerah himpunan penyelesaiannya yang diketahui? Untuk itu simaklah beberapa contoh di bawah ini.

Contoh: Daerah yang diarsir di bawah ini merupakan daerah himpunan penyelesaiaan dari suatu sistem pertidaksamaan linear dua peubah. Tentukanlah sistem pertidaksamaan tersebut.

Penyelesaian:

1. Garis l1 melalui titik (2,0) dan (0,2), persamaan garis l1 adalah:

x/2 + y/2 = 1 menjadi x+y=2

Garis l2 melaui titik (1,0) dan (0,2), persamaan garis l2 adalah:

x/1 + y/2 = 1 menjadi 2x+y=2

Dari gambar terlihat bahwa daerah himpunan penyelesaian (yang diarsir) berada di bawah garis l1, di atas garis l2, di kanan sumbu Y, dan di atas sumbu X. Sistem pertidaksamaannya adalah:

x + y ≤ 2, 2x + y ≥ 2, x ≥ 0, dan y ≥  0

1. Garis l1 melalui titik (4,0) dan (0,4), persamaan garis l1 adalah:

x/4 + y/4 = 1 menjadi x+y=4

Garis l2 melalui titik (2,0) dan (0,–1), persamaan garis l2 adalah:

x/2 + y/-1 = 1 menjadi -x+2y = -2

x-2y  = 2

Dari gambar terlihat bahwa daerah himpunan penyelesaian (yang diarsir) berada di bawah garis l1, di atas garis l2, di kanan sumbu Y, dan di atas sumbu X. Sistem pertidaksamaannya adalah:

x + y ≤ 4, x – 2y ≤ 2, x ≥ 0, dan y ≥ 0

Nilai Optimum Dari Sistem Pertidaksamaan Linier.

Dengan mengetahui cara menentukan daerah penyeleseaian sistem pertidak samaan dan cara membuat model matematika, maka nilai optimum dari masalah program linear dapat dipecahkan dengan mudah. Adapun langkah-langkahnya sebagai berikut:

1. Menentukan model matematika
2. Menentukan daerah penyelesaian
3. Menentukan titik-titik pojok dari daerah penyelesaian tersebut
4. Menentukan nilai optimum daerah penyelesaian dengan cara membandingkan hasil subtitusi titik-titik pojok terhadap fungsi objektif yang telah dicari dengan menggunakan model matematika.

Contoh (contoh minggu lalu):

Harga sebuah  baju Rp. 25.000 sedangkan sebuah celana Rp.50.000. modal yang tersisa Rp.1.500.000. kapasitas took tersebut maksimal memuat 50 buah. Tentukan model matematika untuk memperoleh keuntungan yang sebesar-besarnya, jika laba untuk baju Rp.3.000 dan untuk celana Rp.2.000?

Jawab:

1. Model matematika

Misalkan x= banyaknya baju dan y= banyaknya celana.

	Jumlah barang	harga	laba
Baju (x)	1	Rp. 25.000	Rp.3.000
Celana (y)	1	Rp.50.000	Rp.2.000
Jumlah	50	Rp.1.500.000.	Fobj

Model matematika:

1. Fungsi Kendala

x + 2y ≤ 60; x+ y ≤50; x ≥ 0; y≥0

1. Fungsi Objektif

F(x,y) = 3.000x + 2.000y

2. Daerah penyelesaian
3. Bentuk persamaan dari sistem pertidaksamaan di atas adalah

x + 2y = 60; x+ y =50; x = 0; y=0

1. grafik persamaan di atas dalam koordinat kartesius, sebagai berikut:

titik-titik potong terhadap sumbu-x dan sumbu-y

	x + 2y = 60				x+ y =80
X	0	60		X	0	50
y	30	0		y	50	0
(x,y)	(0,30)	(60,0)		(x,y)	(0, 50)	(50,0)

2.daerah penyelesaiannya

misal kita ambil titik (0,0) [karena titik (0,0) di luar garis x + 2y = 60 dan x+ y =50

subtitusi (0,0) ke pertidaksamaan di atas

subtitusi (0,0) ke  x + 2y ≤ 60 dan x+ y ≤50

0 + 2.0 ≤ 60 dan 0 + 0 ≤50

0 ≤ 60 dan 0 ≤50 (benar)

sehingga arsir daerah yang tidak memuat titik (0,0).

3. Titik-titik pojok dari daerah penyelesaian

A(0,0), B(50,0), C(0,30) dan D (?,?)

Titik D dapat dicari dengan mengeliminasi sistem persamaan di atas, yaitu x + 2y = 60 dan x+ y =50

x + 2y = 60
x+ y =50	–
y=10

Sehingga x+ y  =50

x+ 10 =50

x   = 50 – 10

x   = 40

titik D(40, 10)

4. Nilai optimum

Nilai optimum( maksimum) dapat dicari dengan membandingkan hasil subtitusi titik-titik pojok ke fungsi objektif.

Titik pojok		F(x,y) = 3.000x + 2.000y
A	(0,0)	Rp.0
B	(50,0)	Rp.150.000
C	(0,30)	Rp.60.000
D	(40,10)	Rp.140.000

Kesimpulan

Jadi titik optimumnya adalah B(50,0), dengan kata lain untuk memperoleh keuntungan yang maksimal, maka jumlah baju (x) yang dijual ialah 50 buah dan jumlah celana yang dijual 0 buah

CONTOH SOAL UN POGRAM LINER

Soal

1. Seorang pedagang buah-buahan menjual apel dengan modal sebesar Rp. 2.400.000,00. Dia menjual dengan menggunakan gerobak yang dapat menamapung buah-buahan sebanyak 180 kg, Harga beli apel Rp 15.000,00 per kg dan harga jualnya Rp 18.000,00 per kg. Sedangkan jeruk dibeli dengan harga Rp. 12.000,00 per kg dan dijual Rp. 14.000,00. Jika barang terjual semua, keuntungan maksimum yang diperoleh pedagang tersebut adalah ….

(A) Rp. 320.000,00

(B) Rp. 360.000,00

(C) Rp. 420.000,00

(D) Rp. 440.000,00

(E) Rp. 480.000,00

Jawaban :

(D) Rp. 440.000,00

Pembahasan :

Model matematika :

x + y < 180

15.000x + 12.000y < 2.400.000

x > 0

x > 0
z = (18.000 – 15.000)x + (14.000 – 12.000)y

z = 3.000x + 2000y

Untuk mencari keuntungan maksimumnya dilakukan dengan cara mencari titik potong antara  x + y = 180 dan 15.000x + 12.000y = 2.400.000.

Sederhanakan bentuk :

x + y = 180
15.000x + 12.000y = 2.400.000
Maka menjadi :

x + y = 180
15x + 12y = 2.400

x + y = 180
5x + 4y = 800

Untuk mencari x kalikan  x + y = 180 dengan 4, maka

(x + y = 180)x 4
5x + 4y = 800
4x + 4y = 720
5x + 4y = 800

Kemudian kurangi 5x + 4y = 800 dengan 4x + 4y = 720, maka :

5x + 4y = 800
4x + 4y = 720 –
x = 80

kemudian substitusikan x = 80 ke persamaan x + y = 180, maka :

x + y = 180
80 + y = 180
y = 180 – 80
y = 100

Titik potongnya adalah (80, 100)
Maka Keuntungan maksimum terletak ada pada titik potong garis x + y = 180 dan 15.000x + 12.000y = 2.400.000 adalah koordinat (80, 100)

Maka besar keuntungan nya adalah :

z = 3000(80) + 2000(100)

z = 240.000 + 200.000

z = 440.000

2. Seorang pedagang kue akan membuat dua jenis kue. Setiap kue A menggunakan modal Rp2.000,00 dan dijual mempunyai keuntungan Rp1.000,00 per buah, sedang untuk kue B menggunakan modal Rp3.000,00 dan dijual memperoleh keuntungan Rp1.500,00 per buah. Modal yang tersedia adalah Rp1.200.000,00 dan paling banyak hanya dapat membuat 500 kue setiap hari. Jika kue tersebut terjual habis, keuntungan maksimum yang diperoleh pedagang kue tersebut adalah ….

A.   Rp500.000,00
B.   Rp600.000,00
C.   Rp650.000,00
D.   Rp700.000,00
E.   Rp750.000,00

pembahasan
Tabel bantuan untuk soal di atas:

Kue A (x)
Kue B (y)
500
Modal
2.000
2
3.000
3
1.200.000
1.200
Keuntungan
1.000
1.500
?

Model matematika yang dapat diperoleh dari tabel bantuan tersebut adalah:

x + y = 500         … (1)
2x + 3y = 1.200  … (2)
z = 1.000x + 1.500y

Mari kita eliminasi persamaan (2) dan (1). Persamaan (1) kita kalikan dengan 2 agar mempunyai koefisien x yang sama dengan persamaan (2).

2x + 3y = 1.200
2x + 2y = 1.000
——————— −
y = 200

Selanjutnya kita substitusikan y = 200 ke persamaan (1).

x + y = 500
x + 200 = 500
x = 500 − 200
= 300

Dengan demikian nilai z adalah:

z = 1.000x + 1.500y
= 1.000 × 300 + 1.500 × 200
= 300.000 + 300.000  = 600.000

3.Luas daerah parkir 1.760 m2. Luas rata-rata untuk mobil kecil 4 m2dan mobil besar 20 m2. Daya tampung maksimum hanya 200 kendaraan. Biaya parkir mobil kecil Rp1.000,00/jam dan mobil besar Rp2.000,00/jam. Jika dalam satu jam terisi penuh dan tidak ada kendaraan yang pergi dan datang, penghasilan maksimum tempat parkir adalah ….

A.   Rp176.000,00
B.   Rp200.000,00
C.   Rp260.000,00
D.   Rp300.000,00
E.   Rp340.000,00

Tabel bantuan untuk soal di atas:

Mobil Kecil (x)
Mobil Besar (y)
200
Luas Parkir
4
1
20
5
1.760
440
Biaya Parkir
1.000
2.000
?

Model matematika berdasarkan tabel bantuan tersebut adalah:

x + y = 200    … (1)
x + 5y = 440  … (2)
z = 1.000x + 2.000y

Eliminasi persamaan (2) dan (1) diperoleh:

x + 5y = 440
x +   y = 200
—————— −
4y = 240
y = 60

Kemudian kita substitusikan y = 60 ke persamaan (1).

x + y = 200
x + 60 = 200
x = 140

Dengan demikian nilai z adalah:

z = 1.000x + 2.000y
= 1.000 × 140 + 2.000 × 60
= 140.000 + 120.000
= 260.000

4. Luas daerah parkir 1.760 m2. Luas rata-rata untuk mobil kecil 4 m2 dan mobil besar 20 m2. Daya tampung maksimum hanya 200 kendaraan. Biaya parkir mobil kecil Rp 1.000,00/jam dan mobil besar Rp 2.000,00/jam. Jika dalam satu jam terisi penuh dan tidak ada kendaraan pergi dan datang, maka hasil maksimum tempat parkir itu adalah….

A. Rp 176.000,00
B. Rp 200.000,00
C. Rp 260.000,00
D. Rp 300.000,00
E. Rp 340.000,00

mobil kecil sebagai x, mobil besar sebagai y.
Luas parkir 1760 m2:
4x + 20 y ≤ 1760 disederhanakan menjadi
x + 5y ≤ 440…….(Garis I)
Daya tampung lahan parkir 200 kendaraan:
x + y ≤ 200 …………..(Garis II)
Fungsi objektifnya adalah hasil parkiran:
f(x, y) = 1000 x + 2000 y

Membuat Sketsa Garis 1 dan garis 2

Ubah tanda lebih besar atau lebih kecil menjadi tanda sama dengan terlebih dahulu,
Garis 1
x + 5y = 440
Titik potong sumbu x, y = 0
x + 5(0) = 440
x = 440
Dapat titik (440, 0)
Titik potong sumbu y, x =0
0 + 5y = 440
y = 440/5 = 88
Dapat titik (0, 88)
Garis 2
x + y = 200
Titik potong sumbu x, y = 0
x + 0 = 200
x = 200
Dapat titik (200, 0)
Titik potong sumbu y, x =0
0 + y = 200
y = 200
Dapat titik (0, 200)

Menentukan titik potong garis 1 dan garis 2
Untuk menentukan titik potong bisa dengan substitusi ataupun eliminasi.
x + 5y = 440
x + y = 200
____________ _
4y = 240
y = 60
x + y =200
x + 60 = 200
x = 140
Titik potong kedua garis aalah (140, 60)
Uji titik untuk mendapatkan fungsi obektif maksimum:
Masukkan koordinat titik-titik uji / warna merah  ke f(x, y) = 1000 x + 2000 y
Titik (0,0) → f(x, y) = 1000 (0) + 200 (0) = 0
Titik (200,0) → f(x, y) = 1000 (200) + 2000 (0) = 200 000
Titik (0, 88) → f(x, y) = 1000 (0) + 2000 (88) = 176 000
Titik (140,60) → f(x, y) = 1000 (140) + 2000 (60) = 260 000

5.Luas daerah parkir . Luas rata-rata sebuah mobil  dan luas rata-rata bus . Daerah parkir tersebut dapat memuat paling banyak 30 kendaraan roda empat (mobil dan bus). Jika tarif parkir mobil Rp2000,00 dan tarif parkir bus Rp5000,00 maka pendapatan terbesar yang dapat diperoleh adalah …. (Soal Ujian Nasional)

A.     Rp40.000,00
B.     Rp50.000,00
C.     Rp60.000,00
D.     Rp75.000,00
E.     Rp90.000,00

Pembahasan:

Misalkan:

x = banyak mobil
y = banyak bus

Perhatikan tabel di bawah!

Diperoleh dua persamaan:

    

    

Menentukan daerah yang memenuhi pertidaksamaan:

   

Substitusi nilai y = 10 pada persamaan x + y = 30 untuk mendapatkan nilai x.

    

    

    

Koordinat titik B adalah (20, 10)

6.  Biaya produksi satu buah payung jenis A adalah Rp20.000,00 per buah, sedangkan biaya satu buah produksi payung jenis B adalah Rp30.000,00. Seorang pengusaha akan membuat payung A dengan jumlah tidak kurang dari 40 buah. Sedangkan banyaknya payung jenis B yang akan diproduksi minimal adalah dari 50 buah. Jumlah maksimal produksi kedua payung tersebut adalah 100 buah. Biaya minimum yang dikeluarkan untuk melakukan produksi kedua payung sesuai ketentuan tersebut adalah ….

A.     Rp2.000.000,00
B.     Rp2.300.000,00
C.     Rp2.200.000,00
D.     Rp2.100.000,00
E.     Rp2.000.000,00

Pembahasan:

Pemisalan:

x = banyak payung A
y = banyak payung B

Model matematika dari permasalahan tersebut adalah:

Fungsi tujuan: meminimumkan

Fungsi kendala:

Daerah penyelesaian yang memenuhi permasalahan:

Nilai minimim akan diperoleh melalui titik koordinat yang dilalui garis selidik yang pertama kali, yaitu titik A(40, 50). Sehingga, biaya produksi minimum adalah

Jawaban: B

7. Seorang pedagang gorengan menjual pisang goreng dan bakwan. Harga pembelian untuk satu pisang goreng Rp1.000,00 dan satu bakwan Rp400,00. Modalnya hanya Rp250.000,00 dan muatan gerobak tidak melebihi 400 biji. Jika pisang goreng dijual Rp1.300,00/biji dan bakwan Rp600,00/biji, keuntungan maksimum yang diperoleh pedagang adalah…
A. Rp102.000,00
B. Rp96.000,00
C. Rp95.000,00
D. Rp92.000,00
E. Rp86.000,00
Pembahasan
Gorengan jadi x, bakwan jadi y

 

Modelnya:
1000x + 400y ≤ 250000, sederhanakan, bagi 100 dapat persamaan (i)
(i) 10x + 4y ≤ 2500
(ii) x + y ≤ 400
f(x,y) = 300x + 200y

Titik potong garis (i) dan (ii) dengan sumbu x dan y masing-masing: 

                                                  Grafik selengkapnya: 

8. Nilai minimum dari f(x,y) = 4x + 5y yang memenuhi pertidaksamaan 2x + y ≥ 7, x + y ≥ 5, x ≥ 0, dan y ≥ 0 adalah…
A. 14
B. 20
C. 23
D. 25
E. 35

Pembahasan
Langsung cari titik potongnya dulu:
2x + y = 7
x + y = 5
———— −
x = 2
y = 3
Dapat titik A (2, 3)
Berikut grafik selengkapnya: 

Uji titik
f(x, y) = 4x + 5y
A(2, 3) = 4(2) + 5(3) = 23
B(5, 0) = 4(5) + 5(0) = 20
C(0, 7) = 4(0) + 5(7) = 35
Terlihat nilai minimumnya adalah 20.

9. Nilai maksimum f(x, y) = 5x + 4y yang memenuhi pertidaksamaan x + y ≤ 8, x + 2y ≤ 12, x ≥ 0, dan y ≥ 0 adalah …
a.    24
b.    32
c.    36
d.    40
e.    60
PEMBAHASAN:
–    x + y ≤ 8
ketika x = 0, maka y = 8 …. (0, 8)
ketika y = 0, maka x = 8 …. (8, 0)
–    x + 2y ≤ 12
ketika x = 0, maka y = 6 …. (0, 6)
ketika y = 0, maka x = 12 …. (12, 0)
Sehingga, grafik dari pertidak samaan di atas adalah:

Kita cari dulu titik B, yaitu titik potong dua buah garis, yaitu:

subtitusikan y = 4 dalam x + y = 8
x + 4 = 8
x = 4 …. (4, 4)
Jadi, nilai fungsi obyektifnya adalah:
f(x, y) = 5x + 4y
–    titik A (0, 6)
      5x + 4y = 5.0 + 4.6 = 24
–    titik B (4, 4)
      5x + 4y = 5.4 + 4.4 = 20 + 16 = 36
–    titik C (8, 0)
      5x + 4y = 5.8 + 4.0 = 40
Jadi, nilai maksimumnya adalah 40.
JAWABAN: D

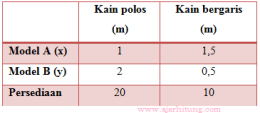
10. Seorang tukang jahit akan membuat pakaian model A dan model B. Model A memerlukan 1 m kain polos dan 1,5 m kain bergaris. Model B memerlukan 2 m kain polos dan 0,5 m kain bergaris. Persediaan kain polos 20 m dan bergaris 10 m. Banyaknya total pakaian jadi akan maksimal jika banyaknya model A dan model B masing-masing…
a. 7 dan 8
b. 8 dan 6
c. 6 dan 4
d. 5 dan 9
e. 4 dan 8
PEMBAHASAN:
Dari soal dapat diresume dalam tabel berikut;

Model matematika yang dapat dibentuk:
x + 2y ≤ 20
1,5x + 0,5 y ≤ 10 atau 15x + 5y ≤ 100
Kita cari titik potong kedua garis tersebut:

subtitusikan x = 4 dalam persamaan x + 2y = 20
4 + 2y = 20
2y = 16
y = 8
maka, banyak model A = 4 dan model B = 8
JAWABAN: E